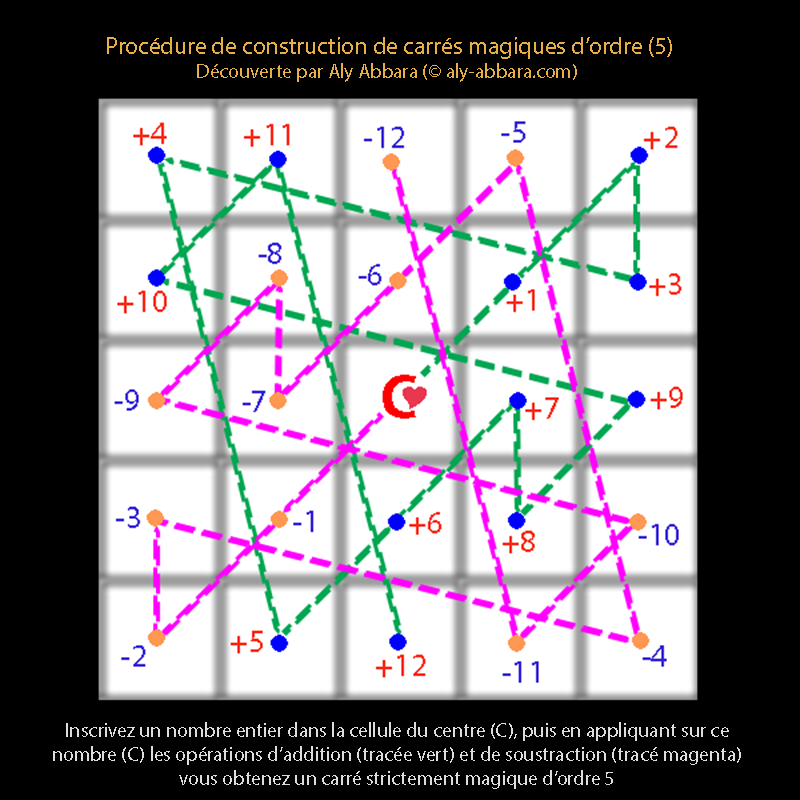
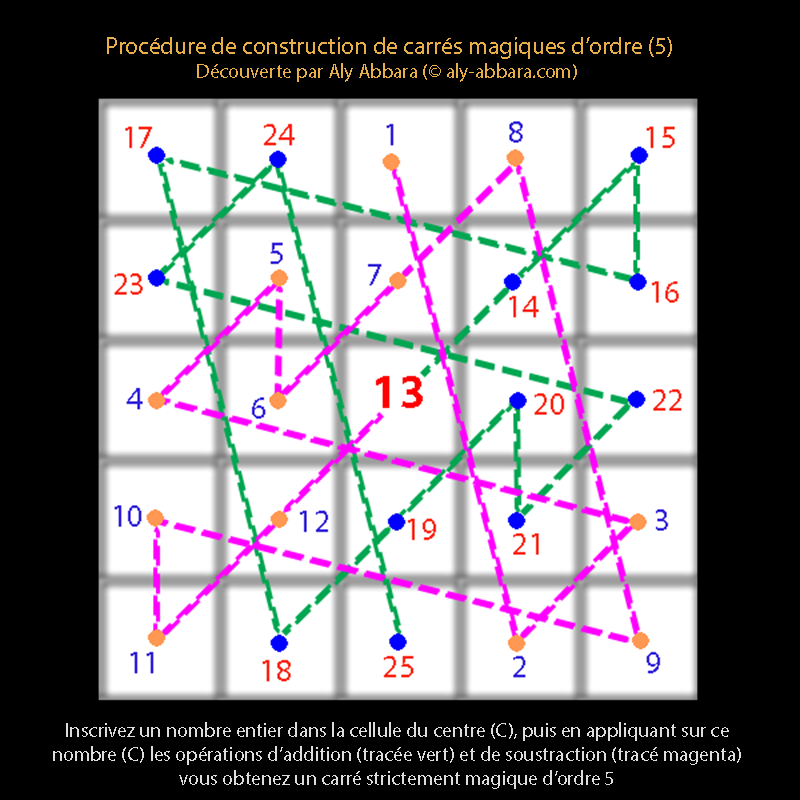
Carrés magiques d'ordre 5 : symétrie orbitale auteur du C, le centre ou le cœur du carré.
Auteur : Aly Abbara - MAJ (
17 Octobre, 2025
)
* Ces carrés magiques se composent de "n" ligne et de "n" colonnes totalisant "n²" de cellules dans lesquelles sont placés "n²" de nombres entiers naturels strictement positifs.
* La qualification "magique" vient du fait que la somme (S) des nombres figurant sur chaque ligne, chaque colonne et chaque diagonale est toujours la même.


|
|---|